Belajar Cara Menemukan Konsep Luas Trapesium
Bangun datar sudah dibelajarkan sejak usia SD kelas 1 melalui tahapan – tahapan sesuai perkembangan anak yang sedang berjalan. Walaupun demikian tidak sedikit anak yang memang belum menguasai dengan baik. Sepertinya anak hanya tahu nama bangunnya saja namun dalam pemahaman masih kurang.
Ada berbagai bagun datar sederhana yang dibelajarkan di SD yaitu : Persegi, Persegi panjang, Jajargenjang, trapesium, layang-layang, belah ketupat, segitiga, dan lingkaran. Dari masing-masing bangun datar tersebut mempunyai sifat-sifat masing – masing.
Berikut kita ulas terlebih dahulu tentang sifat – sifat bangun datar tersebut.
Persegi
Persegi panjang
Jajargenjang
Trapesium
Layang - layang
Belah ketupat
Segitiga
Lingkaran

Demikian sekilas mengingat kembali tentang sifat-sifat bangun datar. Selanjutnya kita kembali ke pokok tujuan utamanya adalah bagaimana cara menemukan konsep luas trapesium agar dapat mudah dimengerti oleh anak?
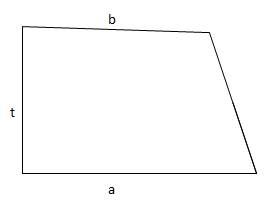
Pertama kita akan gambar sebuah trapesium siku-siku dan kita berasumsi bahwa anak sudah tahu tentang rumus luas segitiga. Lihat gb.
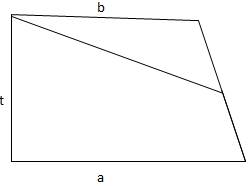
Setelah dibuat gambar seperti gambar kita akan coba buat garis bantu kembali dengan memotong garis miring ditengah-tengah. (lihat gb)
Potong garis tersebut yang baru dibuat dengan rapi dan pisahkan (lihat gb)
Langkah selanjutnya adalah menyatukan hasil potongan tersebut supaya berimpitan (lihat gb)
Gambar yang terbentuk ternyata adalah sebuah segitiga. Masih ingat rumus luas segitiga bukan? Luas segitiga adalah 1/2 x alas x tinggi
Berdasarkan rumus luas segitiga tersebutlah kita akan bisa menemukan konsep luas trapesium. Mari diperhatikan!
Dengan mengajak praktek seperti dijelaskan di atas maka akan lebih mudah memahami konsep luas trapesium dan anak bisa menemukan sendiri pengetahuannya.
Contoh soal:
Misalkan gambar yang tadi diketahui t = 15 cm, a = 20 cm, dan b = 18 cm maka luasnya adalah 1/2 x (20 cm + 18 cm) x 15 cm = 1/2 x 38 x 15 cm2 = 285 cm2.
Demikianlah semoga ada manfaatnya. Dan jangan lupa coment - coment dibawah.
Baca juga :
Ada berbagai bagun datar sederhana yang dibelajarkan di SD yaitu : Persegi, Persegi panjang, Jajargenjang, trapesium, layang-layang, belah ketupat, segitiga, dan lingkaran. Dari masing-masing bangun datar tersebut mempunyai sifat-sifat masing – masing.
Berikut kita ulas terlebih dahulu tentang sifat – sifat bangun datar tersebut.
Persegi
- Memiliki 4 sisi yang sama panjang
- Mempunyai 4 simetri putar, 4 simetri lipat, dan 4 sumbu simetri
- Semua sudut-sudut yang dibentuk siku - siku
Persegi panjang
- Sepasang - sepasang sisi yang sejajar sama panjang
- Memiliki 2 simetri putar, 2 simetri lipat, dan 2 sumbu simetri
- Semua sudut-sudut yang dibentuk siku-siku
Jajargenjang
- Sisi-sisi yang berhadapan sejajar dan sama panjang
- Sudut-sudut yang berhadapan besarnya sama
- Tidak memiliki simetri lipat dan sumbu simetri
Trapesium
- Ada sepasang sisi yang sejajar tetapi tidak sama panjang
- Jumlah sudut yang bersebelahan 1800
Layang - layang
- Memiliki 1 simetri lipat, dan 1 sumbu simetri
- Diagonalnya tidak sama panjang
Belah ketupat
- Semua sisinya sama panjang
- Panjang garis-garis diagonal yang berpotongan sama
Segitiga
- Memiliki 3 sisi
- Mempunyai 3 sudut yang ketika dijumlahkan selalu 1800
Lingkaran
- Sumbu simetri, simteri putar, dan simetri lipatnya tidak terhingga
- Memiliki jari-jari yang sama

Demikian sekilas mengingat kembali tentang sifat-sifat bangun datar. Selanjutnya kita kembali ke pokok tujuan utamanya adalah bagaimana cara menemukan konsep luas trapesium agar dapat mudah dimengerti oleh anak?
Pertama kita akan gambar sebuah trapesium siku-siku dan kita berasumsi bahwa anak sudah tahu tentang rumus luas segitiga. Lihat gb.
Setelah dibuat gambar seperti gambar kita akan coba buat garis bantu kembali dengan memotong garis miring ditengah-tengah. (lihat gb)
Potong garis tersebut yang baru dibuat dengan rapi dan pisahkan (lihat gb)
Langkah selanjutnya adalah menyatukan hasil potongan tersebut supaya berimpitan (lihat gb)
Gambar yang terbentuk ternyata adalah sebuah segitiga. Masih ingat rumus luas segitiga bukan? Luas segitiga adalah 1/2 x alas x tinggi
Berdasarkan rumus luas segitiga tersebutlah kita akan bisa menemukan konsep luas trapesium. Mari diperhatikan!
Dengan mengajak praktek seperti dijelaskan di atas maka akan lebih mudah memahami konsep luas trapesium dan anak bisa menemukan sendiri pengetahuannya.
Contoh soal:
Misalkan gambar yang tadi diketahui t = 15 cm, a = 20 cm, dan b = 18 cm maka luasnya adalah 1/2 x (20 cm + 18 cm) x 15 cm = 1/2 x 38 x 15 cm2 = 285 cm2.
Demikianlah semoga ada manfaatnya. Dan jangan lupa coment - coment dibawah.
Baca juga :




Posting Komentar untuk "Belajar Cara Menemukan Konsep Luas Trapesium"
Kami hanya berbagi informasi, jika ada yang salah atau kurang pas dan ada yang didiskusikan silahkan berkomentar dengan sopan.